Budapesti Műszaki és Gazdaságtudományi Egyetem
Építészmérnöki kar
Építéskivitelezési Tanszék

Többtényezős kiértékelés
(oktatási segédlet)
összeállította: Dr. Klafszky Emil
készítette: Pető Gábor Zsolt (TD)

1. Kiinduló feltételek:

ahol t_ij tábla: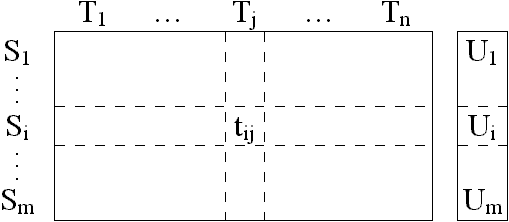

• relatív értékelést tartalmaz
• linealítás teljesül az oszlopokra

tehát igaz rá, hogy:

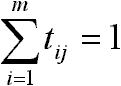
2. A feladat megoldása Klasszikus módszerrel

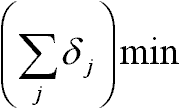
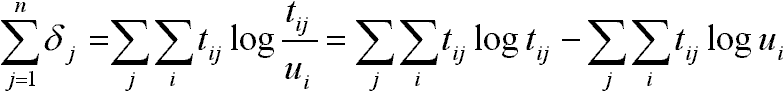
ahol: 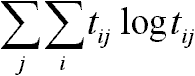  egy fix szám!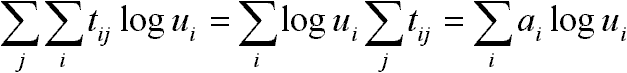

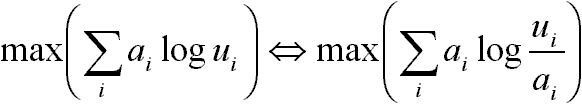
Alkalmazom rá a geometriai egyenlőtlenség 1. végképletét, miszerint:

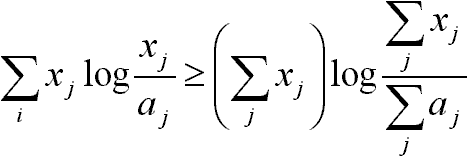
és a relatív értékelés miatt (normálás):

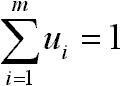
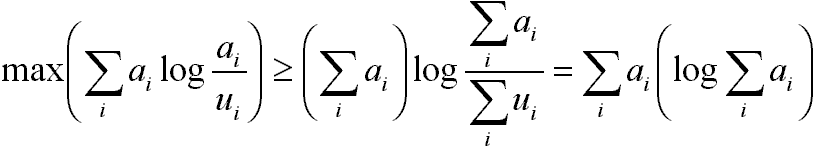
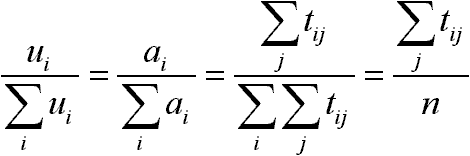
Tehát a véveredmény:

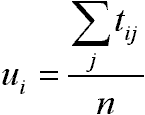
3. A feladat megoldása Arimoto-Blahut módszerrel

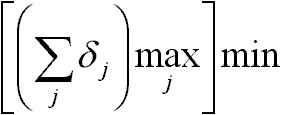
Primál:

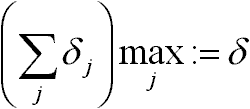
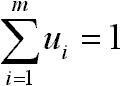
Duál:

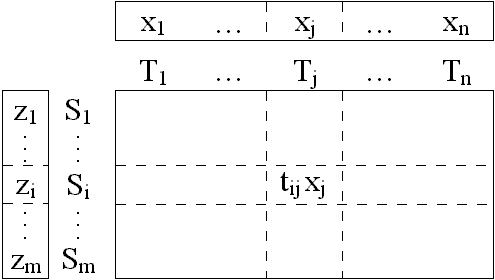
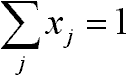
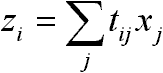
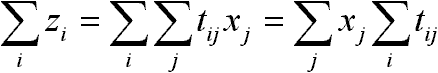
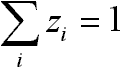
ha z_i és x_j fügettlenek lennének:

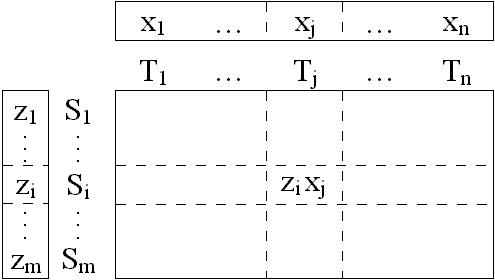
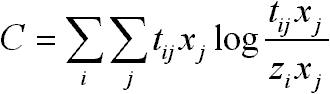
Alapösszefüggés:

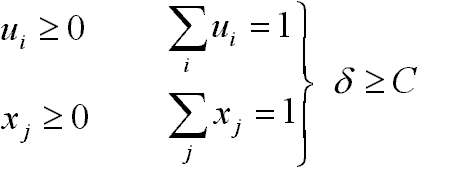
egyenlőség akkor és csak akkor van, ha u_i=z_i minden i-re, és

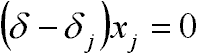 minden j-re.

Bizonyítás:

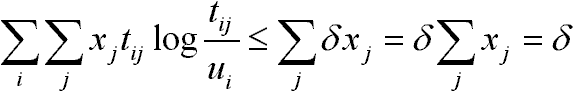
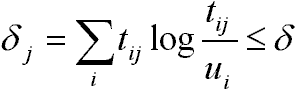
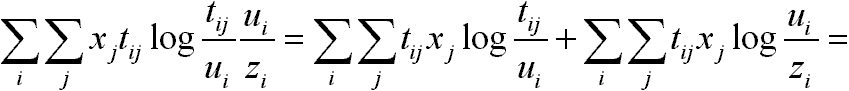
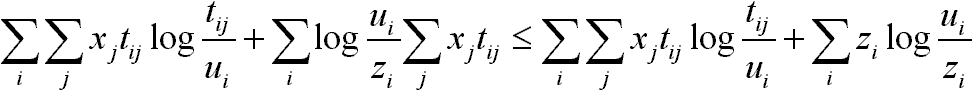
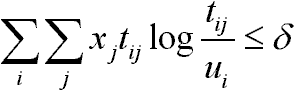
Következmény:

z_i = u_i tehát

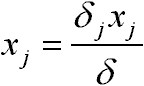
Algoritmus:

segédmennyiség:

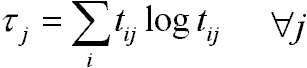
induló érték:

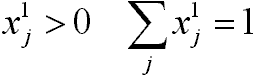
Iteráció:

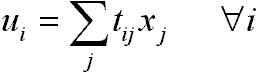
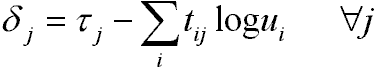
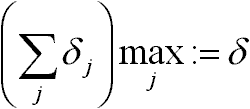
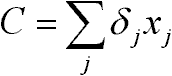
• ha 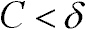akkor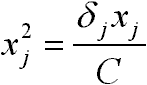
  , és kezdődik az iteráció elölről!
• ha , ahol egy végtelenül kicsi szám,
  akkor a x_i és u_i jó, vége a feladatnak!